Rectified cubic honeycomb

Rectified cubic honeycomb

Type	Uniform honeycomb
Schläfli symbol	t₁{4,3,4}
Coxeter-Dynkin diagrams
Vertex figure	Cuboid
Space group	Pm3m
Coxeter group	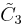${\tilde{C}}_3$ , [4,3,4]
Dual	Square bipyramidal honeycomb
Properties	vertex-transitive, edge-transitive

The rectified cubic honeycomb is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of octahedra and cuboctahedra in a ratio of 1:1.

Octahedron	Cuboctahedron

Symmetry

There are four uniform colorings for the cells of this honeycomb with reflective symmetry, listed by their Coxeter group, and Wythoff construction name, and the Coxeter-Dynkin diagram below.

Symmetry	[4,3,4], 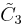${\tilde{C}}_3$	[4,3^1,1], 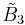${\tilde{B}}_3$	[4,3^1,1], 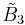${\tilde{B}}_3$	[3^[4]], ${\tilde{A}}_3$
Space group	Pm3m	Fm3m	Fm3m	?
Name	Rectified cubic	Rectified alternate cubic	Cantellated alternate cubic	Birectified quarter cubic
Coloring
Coxeter
Vertex figure

References

George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
Richard Klitzing, 3D Euclidean Honeycombs, o4x3o4o - rich - O15
Uniform Honeycombs in 3-Space: 02-Rich